How many grains of sand are there in the world? It's difficult if not impossible to know this, but instead we can work out how many sand grains there aren't - or at least a figure that we know is greater than the actual number, just to show ourselves (a) that we can do some kind of sensible calculation involving sand, but more importantly (b) that there isn't an infinite number of grains.

Our starting point is an approximation (always start from one of these so your readers can begin to pick holes in your argument straight away - this makes them feel better), that a litre of sand contains about 10 million grains. Since there are 10¹² litres in a cubic kilometre, this gives us a figure of 1 x 10¹⁹ grains per cubic kilometre.

Now, how much sand is on the planet? We don't know and have no way of knowing, so let's set up a reductio ad absurdam which will generate a ballpark total answer to our problem. Imagine that all water in all seas is replaced by sand, like Archimedes said. Average sea depth is 3.7 km, let's take that as a yardstick (eh?). Now fill the space above sea level to the height of the world's tallest sand dune (the Cerro Blanco in Nazca, Peru) which is 2 km above sea level (note - not the highest mountain, Archimedes wasn't so cute there). We have now covered the planet in a layer of sand about 5.7 km thick. This of course is much more than is in fact present on Earth, so we need to make a guess as to what fraction a run a calculation on. We can't guess - is it a millionth, a squillionth, or what? Let's make it easy by dividing by 5.7 so our layer is exactly 1 km thick (readers very pleased now).

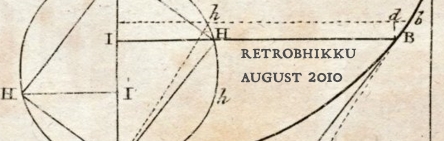
What's the volume of this layer? Assume that the radius of the Earth is 6370 km, add our sand layer and calculate the volume of the whole using the formula 4/3πr³:

(Note to self: Earth volume is about a trillion cubic km). Now do the whole thing again without the sand layer:

Now take one from the other to find the volume of our sand layer, which turns out to be 509,984,416 km³. Or more simply, 5 x 10⁸ km³. Multiplying up by our grains per km³ figure, this gives us a sand layer containing 5 x 10²⁷ grains.

This is about ten thousand times Avogadro's number, so as many sand grains as there are water molecules in ten thousand (small, 18ml) glasses of water. Or if we're out by a factor of ten thousand-ish and our 1 km sand layer was way too thick, there may be only as many sand grains on the planet as there are water molecules in single, small glass of water.

Disappointing.

∞ | comment